weitere infos chaosforschung
Bestellung des im Folgenden wiedergegebenen Textes
als gedruckte Broschüre HIER
Herunterladen als PDF-Datei HIER
Ist die Welt
ein Würfelspiel ?
Entdeckungen
der Chaosforschung
(Joachim Krause)
1. Chaos im
Kosmos?
CHAOS-FORSCHUNG? Dieser Begriff klingt für viele fremd, zum einen nach
(unverständlicher) Wissenschaft, zum anderen nach Durcheinander ...
„Chaos“ ist ein schillernder Begriff, und wir werden bei unserem Thema
auch ganz unterschiedlichen Dingen begegnen: Schmetterlingen und
Wirbelstürmen, einem Mäusevolk auf einer Wiese und Himmelskörpern, die sich im
Kosmos bewegen.
Wir wollen uns zunächst vorsichtig dem Thema nähern. CHAOS – was bedeutet
das eigentlich für mich? Der eine denkt an seinen „Schreibtisch“, der mal
wieder aufgeräumt werden müsste. Einem anderen fällt das Stichwort „Börse“ ein,
an der die Aktienkurse Achterbahn fahren. Ein dritter sagt „Unordnung“, ein
vierter „Kinderzimmer“, „Politik“ wird genannt, von „Zufall“ ist die Rede, vom
„Stau auf der Autobahn“, von „Stress“, oder es wird an das „Tohuwabohu“ im
ersten Kapitel der Bibel erinnert.
Schnell wird deutlich: Wir sind nicht unbelastet. Der Begriff Chaos
verbindet sich für jeden von uns mit konkreten – und sehr unterschiedlichen -
Vorstellungen. Gefühle schwingen mit. Da sind persönliche Bezüge. Manchmal
werden Sorgen deutlich, die Angst vor zu viel Chaos. Chaos verbindet sich mit Unsicherheit,
mit Durcheinander, mit Katastrophen.
Wir werden merken: Das meiste davon hat mit unserem Thema im engeren
Sinne wenig zu tun.
Das Weltbild der Antike kannte die Begriffe KOSMOS und CHAOS als ein Paar
von Gegensätzen. Die alten Griechen sprachen vom Kosmos als der geordneten,
schönen, sicheren Welt, in der wir Menschen uns zurechtfinden und einrichten
können. Chaos dagegen dachte man sich weniger als ein wirbelndes Durcheinander,
sondern stellte sich eher einen dicken grauen Nebel vor, etwas schwer Fassbares
– ohne Form, ohne Struktur, ohne Spielregeln.
Unsere bisherige Vorstellung von der Welt dürfte eher dem antiken Kosmos
entsprechen. Menschen haben in den vergangenen Jahrtausenden immer mehr Ordnung
in der Welt entdeckt. Sie haben begonnen, die erkannten „Spielregeln“
anzuwenden und die Welt erfolgreich nach ihren Vorstellungen zu verändern.
Und nun taucht plötzlich Verunsicherung auf, stellt sich die Frage: Ist
unsere Welt vielleicht doch vom Chaos regiert? Bewegen wir uns in trügerischer
Sicherheit, auf glattem Eis? Selbst Einstein war bei solchen Gedanken unwohl,
und er hat trotzig gemeint: „Gott würfelt nicht!“
Auf jeden Fall ist klar: Seit Darwin im 19. Jahrhundert seine
Vorstellungen von der Evolution der Lebewesen vorstellte, hat kein Versuch der
Erklärung der Natur in der öffentlichen Wahrnehmung so viel Wirbel verursacht,
wie das derzeit die Entdeckungen der Chaosforschung tun. „Chaos“ wird heute in
den unterschiedlichsten Lebensbereichen entdeckt. Wenn sich der Rauch einer
Zigarette über dem Aschenbecher turbulent kringelt, werden Chaos-Vermutungen
geäußert. Wenn das menschliche Herz aus dem Takt gerät und zu „flimmern“
beginnt, beraten sich Mediziner mit Chaosforschern. Wo Plantetenbahnen
vermessen werden, Wirbelstürme ihre Bahn ziehen, wenn es zum Börsen-Crash kommt
oder sich auf der Autobahn aus dem Nichts ein Stau bildet und wieder auflöst –
all das wird unter dem Stichwort Chaos diskutiert. Chemiker und Astronomen,
Philosophen und Komponisten sind fasziniert, Filme nehmen sich des Themas an
(in „Jurassic Park“ warnt natürlich ein Chaosforscher davor, dass das
Experiment mit der Wiederbelebung der Saurierwelt in eine Katastrophe führen
wird). Für Zweieinhalbtausend Mark wurden Wirtschaftsbosse eingeladen, an
einem 2-tägigen Kurs über „Chaos und Management“ teilzunehmen. Chaos in aller
Munde, multimedial vermarktet ... Handelt es sich hier um ein neues
universelles Muster, das uns die Welt endlich richtig erklärt? Oder ist der
ganze Rummel nur eine pseudointellektuelle Modeerscheinung, der nicht zu viel
Gewicht beigemessen werden sollte?
Eine Illusion muss ich Ihnen schon jetzt nehmen. Wir werden bei der
Beschäftigung mit der Chaosforschung keine Lösung finden für das Chaos auf
unserem Schreibtisch oder für Turbulenzen im politischen Geschehen.
Es geht um etwas ziemlich Abstraktes, im Kern um ziemlich nüchterne
Physik und Mathematik – im Physik-Lehrbuch steht das Ganze denn auch unter der
wenig aufregenden Überschrift „Nichtlineare Dynamik“.
Aber – und das ist das Spannende – die neuen Einsichten werfen ganz
erhebliche grundsätzliche Anfragen an unser Weltbild auf.
Im weiteren soll nicht von „der Chaostheorie“ berichtet werden (ein
geschlossenes Theoriegebäude gibt es dazu noch gar nicht), vorsichtiger soll
von überraschenden Entdeckungen berichtet werden, von Chaos-Phänomenen in
unserer Welt, die auch in unserem Alltag eine Rolle spielen.
Wir wollen uns in vier Schritten dem Thema nähern:
Entdeckungen
der Chaosforschung
A)
Das uns
vertraute naturwissenschaftliche Weltbild (siehe
Kapitel 2 und 3)
(Menschen auf der Suche nach Ordnung; der Lauf
der Welt ist berechenbar)
B)
Überraschungen
(siehe Kapitel 4)
(Die Naturwissenschaft stößt auf „Chaos“: Die
Welt entzieht sich der eindeutigen Prognose –
Beispiele: Planetensysteme, Wetter, Bevölkerungs-Entwicklung)
C) Auswirkungen auf unser Weltverständnis (siehe Kapitel 5)
(Die Naturwissenschaft stößt an Grenzen. Der
Mensch kann die Welt nicht umfassend verstehen und in Besitz nehmen. Die
Zukunft der Welt ist offen. Hat das Auswirkungen auf mein Gottesbild?)
D) Warnung vor Scharlatanen und Chaos-Kult (siehe Kapitel 6)
2.
Erinnerung an das vertraute naturwissenschaftliche Weltbild
Wir wollen uns erinnern an das naturwissenschaftliche Weltbild, das in den
letzten Jahrhunderten gewachsen ist, ein beeindruckendes Gebäude aus
Beobachtungen und Theorien.
Dieses Bild von der Welt hat große Erfolge gefeiert, zum einen bei der
Erklärung der Natur, und zum anderen bei ihrer Umgestaltung durch den Menschen
mit Hilfe der Technik.
Das Zeitalter der exakten Naturwissenschaften begann im 16. Jahrhundert.
Nikolaus Kopernikus ordnete die Bewegung der Himmelskörper im Sonnensystem
neu: Nun stand die Sonne im Mittelpunkt, die Erde war ein Planet neben anderen.
Johannes Kepler entdeckte bei seinen Messungen, dass die Planeten auf
elliptischen Bahnen um die Sonne laufen, und er konnte die Bahnen berechnen.
Über hundert Jahre später fasste Isaac Newton die Mechanik der Welt in
allgemein gültige mathematische Gleichungen. Er ging davon aus, dass auf der
Erde wie im (physikalisch zugänglichen) Himmel die gleichen Naturgesetze
gelten. Auf welcher Bahn ein Apfel vom Baum fällt, wie sich zwei Billardkugel
nach der Karambolage (dem Zusammenprall) bewegen, auf welchen Bahnen Planeten
um die Sonne kreisen – all das ließ sich immer exakter messen und auch immer
besser in seinem Verhalten vorausberechnen. Wo noch Ungenauigkeiten auftraten,
herrschte zunehmend die Überzeugung: den Rest zu erklären, war nur eine Frage
der Zeit. Genauere Daten, verbesserte Formeln würden letztlich die ganze Welt
eindeutig berechenbar machen. Überraschungen konnte es eigentlich nicht mehr
geben!
Die
Arbeitsweise der klassischen Naturwissenschaft stellt sich etwa so dar:
·
Menschen sind neugierig. Sie möchten die Welt, die
Natur, immer besser verstehen, und sie möchten sie in den Griff bekommen.
·
Aus der ganzen großen Wirklichkeit der Welt wird ein
interessierender einzelner Aspekt ausgewählt. Alle anderen Faktoren (auch der
Mensch als Beobachter) werden ausgeblendet. Das Weglassen von
„Nebensächlichkeiten“, das Ausblenden von „Störungen“ gehört dabei durchaus zur
Methode der naturwissenschaftlichen Arbeit.
·
Wir beobachten
entweder Vorgänge in der Natur, die sich regelmäßig wiederholen (z.B.
Planetenbahnen)
oder wir gestalten im Labor-Experiment einen Versuch als wiederholbaren Ablauf.
·
Unsere Erwartung ist: Wenn gleiche
Ausgangsbedingungen gegeben sind, läuft der Vorgang in gleicher Weise ab und
führt zum gleichen Ergebnis. Und da zu 100 Prozent gleiche Bedingungen in der
Praxis nicht gegeben sind, wird sogar davon ausgegangen, dass dieses
„Kausalitäts-Prinzip“ in seiner „starken“ Form gültig ist: „Ähnliche Ursachen
rufen ähnliche Wirkungen hervor“.
·
Wir entdecken Regelmäßigkeiten, können „Regeln“
ableiten, nach denen sich die Natur verhält („Naturgesetze“).
·
Die in der Natur gemachten Beobachtungen werden in
die Sprache der Mathematik gefasst, in Formeln.
·
Unsere Erwartung ist: Die Formeln beschreiben die
Wirklichkeit. Wenn wir die Ausgangsbedingungen exakt genug erfassen, ergibt
sich in Berechnungen das zukünftige Verhalten der untersuchten Systeme.
·
Es wächst die Überzeugung, dass es grundsätzlich
möglich ist,
+ die Welt in jedem Detail naturwissenschaftlich zu beschreiben und zu erklären
+ die Dynamik von Systemen, ihre zukünftige Entwicklung exakt vorherzuberechnen
+ in den Ablauf von Naturvorgängen einzugreifen und sie zielgerichtet zu
verändern.
3. Die Welt als berechenbares Uhrwerk
Im Verständnis der klassischen Physik erscheint die Welt als
Uhrwerk. Der Philosoph und Physiker Pierre Simon de Laplace brachte dieses
Weltverständnis 1776 in ein Bild. Er stellte sich vor, dass, wenn ein „Dämon“
(ein
„Eine Intelligenz, welche
für einen gegebenen Augenblick alle in der Natur wirkenden Kräfte sowie die
gegenseitige Lage der sie zusammensetzenden Elemente kennte, und überdies
umfassen genug wäre, um diese gegebenen Größen der Analysis zu unterwerfen,
würde in derselben Formel die Bewegungen der großen Weltkörper wie des
leichtesten Atoms umschließen; nicht würde ungewiss sein und Zukunft wie
Vergangenheit würden ihr offen vor Augen liegen.“
(Pierre Simon de Laplace 1814)
superintelligenter Geist) für einen einzigen Augenblick der
Weltgeschichte in der Lage wäre, den genauen Aufenthaltsort aller Körper im
Universum zu bestimmen wie auch die Kräfte, die auf diese Körper einwirken –
dass dieser Dämon mit seiner Kenntnis der Naturgesetze genaue Aussagen machen
könnte über jeden beliebigen Zustand der Welt in der Vergangenheit oder in der
Zukunft. Alles in dieser Welt wäre danach eindeutig und für alle Zeiten festgelegt
(determiniert).
Die klassische Naturwissenschaft sah es als ihre Bestimmung
an, nach und nach in die Rolle des „Laplace´schen Dämons“ zu schlüpfen ...
Die Welt begegnet in dieser Sichtweise als berechenbares
Uhrwerk. Der Lauf der Welt ist vorherbestimmt, festgelegt durch die geltenden
Naturgesetze und durch die Anfangsbedingungen.
Wie geht es mir mit diesem Weltbild? Kommt es mir bekannt
vor, ist es vielleicht auch mein Weltbild?
Gibt mir eine berechenbare Welt Sicherheit? Oder ist mir eine solche Welt
unheimlich, in der Willensfreiheit nur eine Illusion sein kann?
Das mechanistische Weltverständnis von der Welt als Uhrwerk war das
Weltbild der Naturwissenschaften bis ins 20. Jahrhundert hinein. Erste
Fragezeichen tauchten schon vor hundert Jahren auf. Es zeigte sich, dass die
klassische Physik Newtons nicht ausreichte, um die ganze Wirklichkeit zu
fassen. Die Theorien erwiesen sich nicht als falsch, aber als
ergänzungsbedürftig. Auch heute noch fliegen die Satelliten, die wir in den
erdnahen Orbit schicken, zuverlässig nach Newtonschen Gleichungen. Aber wenn
es um das Verständnis des Universums in seinen wirklichen Dimensionen geht
oder um die Beschreibung der Welt der Elementarteilchen – dann reichen die
physikalisch-klassischen Vorstellungen von der Welt nicht aus.
Wir wissen heute: Die Welt besteht nicht nur aus Teilchen, die einander
herumstoßen (das aber war die Grundvorstellung Newtons), es gibt auch Wellen,
Felder, Teilchen ohne Masse, die so nicht zu (er-)fassen sind.
Ergänzungsbedürftig erwies sich die klassische Physik zum einen in
kosmischen Dimensionen. Dort zeigte sich, dass Raum und Zeit keine absoluten
Größen sind. Auch Masse und Energie sind nicht von grundsätzlich verschiedener
Qualität, sondern können prinzipiell ineinander umgewandelt werden (E=mxc2).
In atomaren Größenordnungen wiederum zeigte sich, dass die erreichbare
Genauigkeit unserer Beobachtungen (die Erfassung der Ausgangsbedingungen) an
Grenzen stößt. Wenn wir sehr kleine Teilchen – z.B. Elektronen – beobachten und
vermessen wollen, verändern die Teilchen der zur Messung benutzten Strahlung
den Zustand des Beobachtungsobjekts; Photonen prallen auf das Elektron und
verändern seine Lage oder seine Geschwindigkeit. Der Ort, an dem sich ein
Teilchen gerade befindet (z.B. ein Elektron auf seiner Bahn um den Atomkern)
und die Geschwindigkeit (der Impuls), mit der es sich im Moment bewegt, lassen
sich so nicht gleichzeitig genau bestimmen. Wenn wir die Geschwindigkeit auf 1
km/h genau kennen, ergibt sich eine „Unschärfe“ der Ortsbestimmung von 3 mm!
Eine letzte Ergänzung: In der Natur gibt es den absoluten Zufall (übrigens:
wenn Naturwissenschaftler von „Zufall“ sprechen, ist das für sie keine metaphysische
oder existenzielle Aussage, sondern soll lediglich aussagen: Wir haben für
dieses Phänomen keine rationale Erklärung). Wenn wir ein radioaktives Atom
beobachten, kann es in der nächsten Sekunde zerfallen, dieses Ereignis kann
aber auch erst nach Millionen von Jahren eintreten. Für das einzelne Atom, das
Individuum, kann die Physik keine eindeutige Vorhersage machen. Anders verhält
es sich, wenn eine große Anzahl von Atomen der gleichen Art betrachtet wird –
dann gibt die Halbwertzeit sehr exakt an, nach Ablauf welcher Zeit die Hälfte
der beobachteten Atome zerfallen ist (mit dieser statistischen Aussage lässt
sich wieder gut rechnen).
Damit hatte die Physik schon in der ersten Hälfte des 20. Jahrhunderts
gezeigt, dass der immer und überall erwarteten Berechenbarkeit der Welt
Grenzen gesetzt sind.
Aber das betraf weithin Bereiche, die weit von der Alltagserfahrung des
Menschen entfernt sind, kosmische oder atomare Dimensionen. Nun aber behauptet
die Chaosforschung, dass sogar in unserer normalen Alltagswelt vieles nicht
eindeutig berechenbar ist.
4. Die
Naturwissenschaft erlebt Überraschungen
An drei Beispielen soll verdeutlicht werden, wo die Wissenschaft auf
Chaos gestoßen ist. Es wurden drei sehr unterschiedliche Bereiche ausgewählt:
zum ersten der Ausgangspunkt der klassischen Physik, der Lauf von Planeten um
ihre Sonne, zum zweiten die Möglichkeit der Berechnung zuverlässiger
Wetterprognosen und zum dritten die Entwicklung eines Mäusevolkes auf einer
Wiese.
4.1. Wie stabil
ist unser Planetensystem?
Im Jahre 1885 setzte der schwedische König einen Preis aus für die
(wissenschaftliche) Beantwortung der Frage: „Wie stabil ist eigentlich unser
Planetensystem?“. Unser Heimatplanet Erde zieht zusammen mit 8 weiteren Planeten
seit unendlichen Zeiten auf seiner Bahn um die Sonne. Können wir uns darauf
verlassen, dass das auch in Zukunft immer so bleiben wird, oder könnte diese
kosmische Harmonie (von der unser Leben abhängt) irgendwann aus dem
Gleichgewicht kommen?
Der französische Mathematiker und Naturwissenschaftler Henri Poincare
nahm entsprechende Berechnungen vor – und stieß bald auf unerwartete
Schwierigkeiten. Er begann zunächst mit dem einfachsten Modell: zwei
Himmels-Körper, Sonne und Erde, die aufeinander einwirken. Für diesen Fall
lieferten die Gleichungen der klassischen Physik klare Aussagen und eindeutige
Ergebnisse für alle Zukunft. Aber schon bei der Betrachtung von drei Körpern
tauchten Schwierigkeiten auf. Wenn man beispielsweise das Zweiersystem
Sonne-Erde um einen dritten Körper (z.B. Jupiter) ergänzt, gibt es
Ausgangssituationen in der Konstellation der drei Himmelskörper, bei denen
geringste Veränderungen (Abstände, Masse, Stellung der Himmelskörper
zueinander) sich unerwartet stark auf das Ergebnis der Berechnungen auswirken.
Poincare stellte schon für den noch relativ einfachen Fall solcher
Drei-Körper-Systeme fest, dass die bisher vorausgesetzte generelle
Berechenbarkeit der Welt nicht immer gegeben ist. Newton hatte mit seiner
Formulierung der Bewegungsgleichungen den Eindruck erweckt, dass damit das
gesamte Universum mathematisch beschrieben sei. Aber das Aufschreiben der
Gleichungen war das eine, aus ihnen (eindeutige) Lösungen zu erhalten, offenbar
etwas ganz anderes. Auch Forscher vor Poincare waren auf diese Schwierigkeiten
gestoßen. Sie hatten versucht, den Einfluss weiterer Planeten auf
Zweikörpersysteme als „Störung“ pauschal zu berücksichtigen (als Faktor, der
zusätzlich in die Berechnung eingeht und sie - mehr oder weniger genau –
korrigiert).
„Eine sehr kleine Ursache, die wir nicht bemerken, bewirkt einen
beachtlichen Effekt, den wir nicht übersehen können, und dann sagen wir, der
Effekt sei zufällig. Wenn die Naturgesetze und der Zustand des Universums zum
Anfangszeitpunkt exakt bekannt wären, könnten wir den Zustand dieses Universums
zu einem späteren Moment exakt bestimmen. Aber selbst wenn es kein Geheimnis in
den Naturgesetzen mehr gäbe, so könnten wir die Anfangsbedingungen doch nur
annähernd bestimmen. Wenn uns dies ermöglichen würde, die spätere Situation in
der gleichen Näherung vorherzusagen – dies ist alles, was wir verlangen -, so
würden wir sagen, dass das Phänomen vorhergesagt worden ist und dass es
Gesetzmäßigkeiten folgt. Aber es ist nicht immer so; es kann vorkommen, dass
kleine Abweichungen in den Anfangsbedingungen schließlich große Unterschiede in
den Phänomenen erzeugen. Ein kleiner Fehler zu Anfang wird später einen großen
Fehler zur Folge haben. Vorhersagen werden unmöglich, und wir haben ein
zufälliges Ereignis.“
(Henri Poincare; Ende des 19. Jahrhunderts)
Die Ergebnisse seiner Berechnungen waren für ihn „so bizarr, dass ich es
nicht aushalte, darüber nachzudenken ...“.
Poincare erhielt im Jahre 1890 das Preisgeld, obwohl er die eigentlich
gestellte Frage nicht beantwortet hatte. Er konnte nicht nachweisen, dass die
Erdbahn für alle Zeiten stabil sein würde, sondern seine Untersuchungen säten
gerade den Zweifel am ewigen Gleichlauf der Planeten. 300 Jahre lang hatten
die Planetenbewegungen als Inbegriff der Gleichmäßigkeit gegolten, und für die
Naturwissenschaftler waren sie das Musterbeispiel für Vorhersagbarkeit
in der Natur. Und nun erwies sich die Welt des Menschen als unsicherer, als man
bisher gemeint hatte. Schon die Berechnung eines den Physikern gut bekannten
und relativ übersichtlichen mechanischen Systems entzog sich der exakten
Prognose.
Die von Poincare aufgedeckte Unsicherheit war übrigens keine Frage
unzulänglicher Daten oder mathematischer Möglichkeiten vor 100 Jahren. Auch
moderne Computer helfen hier nicht weiter. Auch sie zeigen nur, dass unsere
mathematischen Gleichungen für die Beschreibung der Welt manchmal sehr
empfindlich reagieren.
Der Abstand zwischen Erde und
Sonne beträgt etwa 150 Millionen Kilometer und kann derzeit mit einer Genauigkeit
von + 15 Meter genau bestimmt werden. Diese minimale Unsicherheit bei
der Vermessung der Erd-Bahn schaukelt sich bei der Berechnung von vielen
Umläufen so auf (unter dem Einfluss der Sonne und der anderen Planeten), dass
die Position der Erde nach 100 Millionen Jahren völlig ungewiss ist: Sie kreist
zwar noch immer um die Sonne, aber ihr Aufenthaltsort ist völlig unsicher, er
kann irgendwo auf der Umlaufbahn liegen.
Wenn diese Unsicherheit erst nach 200 Millionen Jahren auftreten soll, müssten
wir den Abstand Erde-Sonne auf 10-10 cm (das entspricht dem
Durchmesser eines Atoms) genau bestimmen; diese Mess-Ungenauigkeit „schaukelt“
sich in den Berechnungen über lange Zeiträume zu kosmischen Größenordnungen
auf.
Moderne
Berechnungen bestätigen auf der einen Seite das Grundsätzliche der neu
entdeckten Unsicherheit, haben aber (in der Beantwortung der königlichen
Preisfrage) auch zeigen können, dass unser Planetensystem im wesentlichen doch
recht stabil ist. Zumindest für die nächsten 10 Millionen Jahre lässt sich die
Umlaufbahn der Erde berechnen, danach ist die Position der Erde schlicht
unbestimmt. Das heute beobachtbare Planetensystem erweist sich doch als recht
robust. Wenn es in der Vergangenheit weitere Kandidaten gegeben haben sollte,
die auf besonders anfälligen, instabilen Bahnen unterwegs waren, sind diese
wahrscheinlich vor langer Zeit entweder von anderen Planeten eingefangen oder
aus dem Sonnensystem herausgeschleudert worden.
Seit
Poincares Berechnungen war eine unbequeme Einsicht in der Welt: die klassische
Physik liefert nicht einmal für die recht einfachen Verhältnisse im Kosmos
eindeutige Prognosen.
Aber bei
der Berechnung von Planetenbahnen für die nächsten Jahrmillionen handelte es
sich doch um recht abstrakte mathematische Überlegungen, weit weg vom Alltag.
Anfang der
1960er Jahre wurde es praktischer mit der Chaosforschung, sie rückte näher an
den Alltag heran.
„Chaos“ ist ein
schillernder Begriff, der für verschiedene Menschen mit sehr unterschiedlicher
Bedeutung gefüllt ist. Zwei Mathematiker führten ihn 1975 in einer
Fachzeitschrift als Fachbegriff ein („Period Three Implies Chaos“), um das
„empfindliche“ Verhalten von bestimmten mathematischen Formeln zu
charakterisieren, die bei geringsten Veränderungen der Ausgangsgrößen völlig
unterschiedliche Ergebnisse für zukünftige Entwicklungen liefern können.
Verschiedene Formen
von Kausalität
Das (normale) Kausalgesetz geht davon aus, dass „gleiche
Ursachen gleiche Wirkungen haben“. Da in der Praxis der Naturwissenschaft bei Beobachtungen
und bei Experimenten in der Regel eine 100-prozentige Gleichheit der Ursachen
nicht festgestellt oder hergestellt werden kann, wird sogar von der Gültigkeit
des Kausalgesetzes in seiner „starken Form“ ausgegangen
(„Ähnlichkeitsprinzip“): dass nämlich „ähnliche Ursachen zu ähnlichen Wirkungen
führen“ (wen ich bei einem zweiten Pistolenschuss ähnlich genau ziele wie beim
Schuss vorher, landet der zweite Treffer in der Nähe des ersten). Offenbar gibt
es aber in der Natur eine andere Form der Kausalität, für die das
Ähnlichkeitsprinzip hinsichtlich Ursache und Wirkung nicht mehr gültig ist.
Unter bestimmten Umständen „können ähnliche Ursachen gänzlich unterschiedliche
Wirkungen haben“. Systeme, in denen diese Form der Kausalität angetroffen wird,
bezeichnet man in der Physik als „chaotisch“.
Chaos kann auch im
Computer entstehen
Das Ergebnis von Berechnungen über zukünftige Entwicklungen ist unter Umständen
gar nicht von der Genauigkeit der verwendeten Größen abhängig, sondern wird
schon von der Rechengenauigkeit des Computers beeinflusst.
Ein Beispiel: Ein Komet kommt aus der Tiefe des Raumes,
gerät in das Schwerefeld der Sonne und wird auf eine Umlaufbahn gezwungen.
Zusätzlich wird er noch hin und wieder vom Schwerefeld eines dritten Körpers, des
Jupiters, beeinflusst. Wenn man einen Computer einsetzt, der seine
Zwischenergebnisse auf 6 Stellen genau rundet, ergeben sich für den Kometen 757
Umläufe um die Sonne, ehe er wieder in Richtung Weltall abdriftet. Ein genauer
rechnender Computer, der immer 7 Stellen übernimmt, berechnet nur 38 Umläufe.
Ein anderer Computer, der noch exakter immer auf 8 Stellen genau rechnet, kommt
auf 236 Umläufe ...
Ein zweites Beispiel: An zwei Universitäten wurde das
gleiche Dreikörperproblem berechnet: ein kleiner Planet umkreist in einem
Doppelsternsystem zwei Sonnen. An der Universität in Bremen ergaben sich
schnell chaotische Umlaufbahnen. In Karlsruhe aber lief der Planet auf
beruhigend konstanter Bahn. Die Erklärung: im zweiten Fall hatte man feinere
Zeitschritte gewählt.
4.2. Wie sieht
das Wetter in drei Wochen aus?
Edward
Lorenz, ein Wetter-Mathematiker am MIT in Boston/USA, saß 1963 an seinem
Computer. Sein Ziel war es, langfristige Wetter-Prognosen in Zukunft noch
besser berechnen zu können.
Das
Wettergeschehen, so meinte man damals, sollte eigentlich physikalisch eindeutig
zu beschreiben sei. Bei den Vorgängen in der Atmosphäre (z.B. Temperatur- und
Druckverhältnisse, Geschwindigkeit und Richtung von Luftströmungen) handelt es
sich um die Dynamik und die Zustandsänderungen von Gasen, wie sie aus der
Strömungslehre und aus der Thermodynamik schon lange bekannt sind.
Lorenz hatte ein grobes Modell der Erdatmosphäre für recht einfache
Verhältnisse in seinen Rechner eingegeben: eine größere Region im Nordatlantik,
also ohne störende Einflüsse durch Küsten oder Gebirge. Seine Beschreibung des
„Wetters“ bestand aus drei Gleichungen, die Strömungs-Vorgänge und
Wärmeleitungs-Prozesse beschrieben.
dx
dy dz 8
---- = -10x +10y ; ---- = 28x –y
–xz ; ----
= --- z + xy
dt
dt dt 3
x,
y und z stehen dabei für Umweltparameter, man könnte sich also grob z.B.
Messgrößen für Temperatur, Luftfeuchtigkeit oder Windgeschwindigkeit
vorstellen. dt gibt die Veränderungen im Zeitablauf an. Das Ganze sieht recht
übersichtlich aus, sollte mathematisch gut lösbar sein, und so war auch Lorenz
guten Mutes, als er den Computer startete. Sein Computer arbeitete 1963 noch
sehr langsam (17 Rechenschritte pro Sekunde), sodass Stunden vergingen, in
denen der Tintenschreiber langsam eine Kurve für das berechnete „Wetter“
aufzeichnete (siehe die ausgezogene Kurve in der folgenden Abbildung).
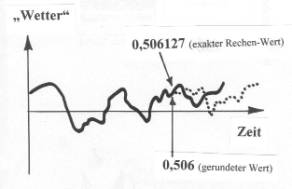Der Computer hatte bereits
zwei Tage gerechnet, als eine ungeplante Unterbrechung eintrat: Die Tinte in
der Kapillare, mit der die Kurve gezeichnet wurde, ging zu Ende. Lorenz brach
den Rechenvorgang ab und füllte Tinte nach. Um nicht zwei Tage zu verlieren,
ging er ein kleines Stück in seinen Rechenergebnissen zurück und setzte den
Tintenschreiber auf die bereits gemalte Kurve aus dem ersten Rechengang auf. Er
erwartete, dass der Verlauf des „Wetters“ zunächst der bekannten Linie folgen
würde und die Rechnung dann problemlos weitergeführt werden könnte. Aber nach
kurzer Zeit zeichnete der Computer einen ganz anderen „Wetter“-Verlauf (siehe
gepunktete Kurve). Bildlich gesprochen: Wo in der ersten Runde die Sonne
geschienen hatte, regnete es nun.
Lorenz
fand bald den Grund für diese Abweichung. Er hatte die Ergebnisse seiner
Berechnungen zwar immer auf 6 Stellen genau zur Verfügung, hatte aber für den
Start zur zweiten Rechenrunde den exakten Wert (0,506127) nach den üblichen
Rechenregeln auf 3 Stellen gerundet (0,506) und die neue Rechnung mit diesem
Wert begonnen. Diese minimale Abweichung führte zu den beobachteten
dramatischen Abweichungen beim berechneten Wetterverlauf! Lorenz untersuchte
den Effekt systematisch und stellte fest, dass dieses „Chaos“ in seiner
Rechnung auch mit genaueren Daten nicht grundsätzlich zu beheben wäre, sondern
an der Art der verwendeten mathematischen Gleichungen lag (und damit an der
Komplexität des Gegenstandes „Wetter“, bei dem in Wirklichkeit ja noch weit
mehr als drei Einflussgrößen „mitspielen“).
Lorenz
wird auch das Wort-Bild vom so genannten „Schmetterlingseffekt“ zugeschrieben.
Damit soll deutlich gemacht werden, dass es sein kann, dass der Flügelschlag
eines Schmetterlings (also eine kleine, ganz unscheinbare Ursache) in Boston
oder anderswo auf der Welt der Grund dafür sein kann, dass zwei Wochen später
und tausend Kilometer entfernt in der Karibik ein Wirbelsturm losrast. Das
Bild sollte nicht über-deutet werden: Eine solche Wetter-Änderung kann
(ausgelöst durch kleinste Einflussgrößen wie den Flügelschlag eines
Schmetterlings) in Einzelfällen eintreten. Aber nicht immer sind Schmetterlinge
verantwortlich für Wetterkapriolen, und Ursache wäre auch dann nicht der
einzelne Schmetterling, sondern eine instabile Wetterlage – das Wetter weiß
gewissermaßen selbst noch nicht, wohin es sich entwickeln wird, es gibt verschiedene
Möglichkeiten, und ein kleiner Anstoß reicht, um die endgültige Richtung
festzulegen.
Die
Einsichten von Edward Lorenz waren eine schmerzliche Erfahrung für Wetterforscher
(bereits eine 7-Tages-Prognose gilt heute als sehr gewagt) und sie haben längst
ihren Niederschlag in der täglichen Praxis der Wetterprognose gefunden.
„Schon wenn wir über das Wetter reden, verändern wir es.“
(Cecil Leith, Wetterforscher,
Die Wetterprognosen für
Europa (die wir z.B. in der 20-Uhr-Tagesschau zu sehen bekommen) werden in
Reading in England zentral erstellt. Dort werden zunächst alle verfügbaren
Daten für die Entwicklung des Wettergeschehens in den letzten 24 Stunden
erfasst, mit ähnlichen Wetterlagen aus der Vergangenheit verglichen und dann
werden die Daten in mathematischen Gleichungen zum „Wetter von Morgen“
verarbeitet (der Computer arbeitet mit 1 Milliarde Rechenschritten pro
Sekunde). Aus dieser Rechnung ergibt sich aber zunächst nur das
„Standard-Wetter“. Die erste Rechnung wird nämlich anschließend auf den
Prüfstand gestellt. In etwa 30 geringfügig abweichenden Varianten (die in die
Rechnungen eingehenden Werte für Temperaturen, Luftdruck usw. werden gezielt
verändert) wird getestet, ob das berechnete „Wetter“ robust reagiert und sich
immer in etwa gleich darstellt, oder ob sich (vielleicht auch nur regional)
empfindliche Bereiche zeigen, die zum Chaos neigen, in denen also völlig
unterschiedliche Rechenergebnisse auftreten. Wir erfahren dann auf der
abendlichen Wetterkarte nur etwas zu einigermaßen „sicheren“ Regionen und
Wetterereignissen. In den meisten Fällen ist heute trotz Chaosphänomenen eine
mehrtägige Wetterprognose möglich, weil stabile Wetterlagen vorliegen. Man weiß
aber inzwischen, dass so genannte „Chaos-Hotspots“ ständig um die Erde wandern,
die etwa 20 Prozent der Erdoberfläche erfassen – und in den davon gerade
betroffenen Regionen gestaltet sich die Arbeit von Meteorologen „chaotisch“.
Wettermodelle und
Wettervorhersage
Um Berechnungen zum Wettergeschehen durchzuführen, wird die Erdatmosphäre
in einzelne Zellen aufgeteilt. Ein Gitternetz zergliedert die Atmosphäre z.B.
in 31 Schichten bis 35 Kilometer Höhe, der horizontale Abstand der
Gitterpunkte beträgt 60 Kilometer (das ergibt etwa 60 Millionen Gitterpunkte).
An den einzelnen Eckpunkten werden die physikalischen Größen gemessen (oder aus
den Daten benachbarter Punkte abgeschätzt), in ihrer Veränderungsdynamik
untersucht, und sie gehen als Ausgangsgrößen in die Modell-Berechnungen zur
weiteren Entwicklung des Wetters ein. In Zeit-Intervallen von
15-Minuten-Schritten ergibt sich dann (nach 6 Stunden Rechenzeit in einem
Hochleistungscomputer) z.B. eine 15-Tages-Prognose.
Über Jahrzehnte ist das Messnetz immer mehr verfeinert worden, die
Rechenmodelle wurden ständig verbessert, immer schnellere Computer kamen zum
Einsatz. Trotzdem bleiben Prognosen unsicher. Bei bestimmten Wetterlagen reicht
eine kleine Änderung einer Größe, etwa der Temperatur, aus, um das Rechenergebnis
von 6 Stunden komplett auf den Kopf zu stellen. Wenn man die Messgenauigkeit
der Wetterparameter um den Faktor 10 verbessert, erweitert sich der Zeitraum
einer verlässlichen Vorhersage um nur 1 Tag. Wenn man nochmals um den Faktor 10
genauere Ausgangsdaten zur Verfügung hat, wird wieder nur 1 Tag für genaue
Vorhersage gewonnen.
Bei einer 7-Tages-Prognose geht man heute davon aus, dass in 30% der Fälle eine
Situation vorliegt, die genaue Vorhersagen unmöglich macht. Und bei einer
15-Tages-Prognose ist meist bereits alles dem Zufall überlassen.
Die Wissenschaft entdeckt das Chaos
Wissenschaftler
waren von den Entdeckungen der Chaosforschung doch überrascht. Sie lernten: Es
gibt bei der mathematischen Beschreibung der Natur empfindliche Bereiche, in
denen CHAOS auftreten kann. Die mathematische Definition für „Chaos“ benennt
das „empfindliche“ Verhalten von Gleichungen, mit denen wir die Natur
beschreiben. Bei geringfügigen Veränderungen in den Ausgangsbedingungen kann
sich ein System völlig unterschiedlich entwickeln. Es gibt – zunächst nur
abstrakt in der Rechnung, aber wohl auch in der damit beschriebenen
Wirklichkeit – manchmal „mehrere Zukünfte“ ...
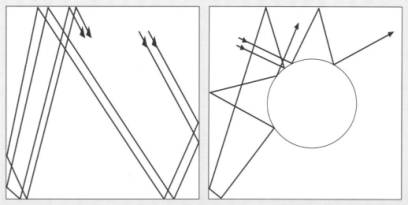Das Ende
der Vorhersagbarkeit?
Ähnliche Ursachen haben zwar oft ähnlich Wirkungen – wie etwa in dem
„quadratischen Billard“ (siehe linke Abbildung). Schon im „Sinai-Billard“
aber, wo die Kugeln gegen einen inneren Kreis stoßen, haben ähnliche Ursachen
ganz verschiedene Wirkungen. Selbst Anfangswerte, die sich nur um wenige Atomdurchmesser
voneinander unterscheiden, sind nach rund einem Dutzend Stößen schon total verschieden.
(aus: Breuer: Der Flügelschlag eines Schmetterlings, 1993 S.81)
Chaos
gibt es heute nicht nur bei Wetterprognosen; Chaos wird inzwischen auch an anderer
Stelle im Alltag entdeckt. Wasserhähne tropfen chaotisch (wenn man einen Wasserhahn
langsam aufdreht, fallen erst einzelne Tropfen in definiertem Abstand, dann jeweils
zwei Tropfen paarweise, später Gruppen von vier Tropfen usw. – bis schließlich
Turbulenzen eintreten und das Ganze sich chaotisch darstellt). Selbst einfache
mechanische Pendel sind nicht exakt berechenbar in ihrem Verhalten (wenn z.B.
auf einer starren Pendelstange ein Gelenk angebracht wird, das den Drehpunkt
für ein zweites Pendel darstellt).
Zeigt sich hier vielleicht nur die Bestätigung alter
Volksweisheiten, wenn Sprichworte sagen: Kleine Ursachen haben große
Wirkungen. Oder: Der Teufel steckt im Detail.
4.3. Wie entwickelt sich ein Mäusevolk auf
einer Wiese?
Im
folgenden geht es um ein „praktisches“ Beispiel aus der Arbeit eines Ökologen. Ein
Biologe möchte berechnen, wie viele Mäuse in den nächsten Jahren auf einer
Wiese leben werden. Er macht dabei Vorgaben, z.B. für die anfängliche
Bevölkerungszahl, für die zur Verfügung stehende Fläche (Lebensraum,
Nahrungsangebot), für Feinde (Raubtiere wie Füchse und Eulen, Krankheiten). Für
die gewünschte Berechnung (Entwicklung der Bevölkerungszahl) gibt es eine
vielfach erprobte Formel (die so genannte „logistische Gleichung). Die
logistische Gleichung verknüpft einen alten Zustand yn (zum
Zeitpunkt n) mit einem neuen Zustand yn+1 (eine Rechen-Runde
später).
Die Überraschung, die in einer
Gleichung steckt ...
Ziel: Berechnung der Entwicklung einer
Tier-Bevölkerung;
bewährtes Mittel zur Beschreibung der Wirklichkeit: die so genannte
„logistische Gleichung“:
yn+1 = a x yn (1 - yn)
Die
Gleichung ist nicht linear – nach Auflösen der Klammer entdeckt man den
quadratischen Anteil:
yn+1 = a x yn - a x yn2
yn =
Bevölkerungszahl am Anfang (0 ... y ... 1)
yn+1 = Bevölkerungszahl
in der nächsten Generation
a = Wachstumsfaktor (abh. von
der Zahl der überlebenden Nachkommen pro Generation; a>1)
n = Zahl der abgelaufenen
Generationen (1; 2; ...
Diese Formel ist ein Beispiel für die mathematische
Beschreibung von Naturvorgängen. In derartigen Gleichungen versucht die
Naturwissenschaft zu erfassen, was sich ausdehnt, bewegt, fortpflanzt,
aufeinander Jagd macht -
also Ameisenvölker, Galaxien, das Wachstum eines Embryos, das nukleare Feuer
einer explodierenden Atombombe. Die mathematische Beschreibung solcher Systeme
zeigt oft zwei Besonderheiten. Zum einen tauchen in den Gleichungen oft
Potenzfunktionen auf (also nicht nur ein Glied x, sondern x2 oder x3).
Zum zweiten hat man es häufig mit Rückkopplungen zu tun; hier geht das Ergebnis
eines Rechenschrittes als Ausgangsgröße in die nächste Rechnung ein usw. usw.
Wenn man beispielsweise Schätzungen für die Weltbevölkerung in 50 Jahren
abgeben will, wird die derzeitige bekannte Zahl von Menschen mit dem
Vermehrungsfaktor multipliziert, der berücksichtigt, um wie viel Prozent
derzeit die Bevölkerung pro Jahr zunimmt, das Rechenergebnis für das Jahr 1
wird in die gleiche Formel als Ausgangsgröße zur Berechnung des Jahres 2
eingesetzt usw.).
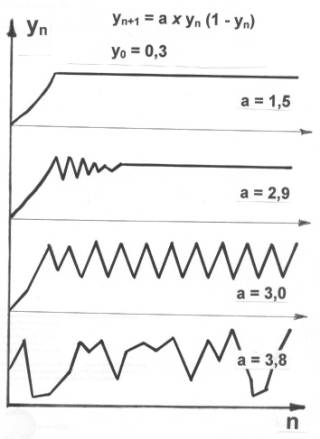Die
logistische Gleichung eignet sich, um die Schwankungen von Tierpopulationen
(Bevölkerungszahl in einem Lebensraum) zu beschreiben. Der Biologe benutzt
also diese vielfach erprobte und bewährte Formel, um die Zahl der Mäuse auf
seiner gedachten Wiese für die nächsten Generationen vorherzusagen. Er setzt
nun Zahlen ein (n = Zahl der Zyklen/Generationen; a = Wachstumsfaktor, der die
Bilanz aus Geburten und Sterbefällen berücksichtigt; y = Zahl der Mäuse in der
Population). In der vorstehenden Grafik ist in der obersten Kurve ein erstes
Ergebnis dargestellt (a wurde mit 1,5 eingesetzt, y mit 0,3). In den ersten
Generationen nimmt die Zahl der Mäuse zu, bis Nahrungsangebot und Feinde ein
weiteres Wachstum begrenzen; es stellt sich langfristig eine stabile
Bevölkerungszahl ein.
Nun verändert der Forscher an seinem Computer eine Größe,
den Wachstumsfaktor a. Dieser wird gesteigert (bildlich gesprochen bekommen
die Mäuse häufiger Nachwuchs). Auch diesmal (siehe zweite Kurve von oben) nimmt
die Bevölkerung anfangs zu, dann schwankt die Zahl der Mäuse einige
Generationen lang, bis sich auch hier ein Gleichgewicht einstellt. Auch eine
solche Bevölkerungs-Entwicklung ist gut vorstellbar.
Bei einer geringfügigen weiteren Erhöhung der Größe a (von
2,9 auf 3,0) ergibt sich ein neues Bild (siehe dritte Kurve). Nach anfänglicher
Zunahme beginnt die Bevölkerungszahl rhythmisch zu schwanken, sie springt
zwischen zwei konkreten Werten hin und her. Auch für ein solches Verhalten
ließen sich in der Natur noch vergleichbare Vorgänge finden. Maikäferpopulationen
z.B. brauchen in unseren Breiten vier Jahre bis zur Entwicklung einer
fortpflanzungsfähigen Generation; daher kommt es hier zu Schwankungen der
Bevölkerungszahl im vierjährigen Rhythmus.
Wenn der Wachstumsfaktor weiter gesteigert wird (siehe
untere Kurve), zeigt die Bevölkerungsentwicklung keine erkennbare Regel mehr,
und die Zahlen schwanken wirklich völlig chaotisch. Hier ist auf der gedachten
„Spiel-Wiese“ offensichtlich ein Zustand erreicht, der keinen einfachen Regeln
mehr gehorcht und aus dem Ruder laufen könnte („Bevölkerungs-Explosion“). Dass
hier das Chaos regiert, zeigt sich auch am nächsten Bild. Hier ist zunächst die
untere Kurve des vorhergehenden Bildes aufgenommen (durchgezogen gezeichnet).
Dort war konkret mit a = 3,8 und y0 = 0,3 gerechnet worden (y0
= Bevölkerungszahl zum Start; vorstellen könnte man sich z.B. 300.000 Mäuse).
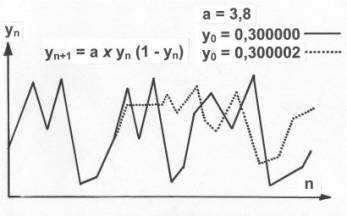Jetzt wird
die Bevölkerungszahl als Eingangsgröße ganz geringfügig verändert, von 0,300000
auf 0,300002 (statt 300.000 Mäuse sind es nun zu Anfang 2 mehr). Die sich nun
ergebende zweite Kurve (gepunktet dargestellt) zeigt, dass in den ersten
Generationen die Entwicklung ähnlich verläuft wie in der ersten Rechnung. Dann
aber ergibt sich ein völlig anderer Kurvenverlauf. Irreguläres Chaos! Selbst
wenn die Abweichungen der Ausgangswerte für y bei nur 0,0000000001 liegen,
ergeben sich deutlich veränderte Abläufe.
Das Ergebnis bedeutet nun aber nicht, dass die verwendete
Formel völlig unbrauchbar wäre. Sie ist weiterhin geeignet, um den Vorgang
„Bevölkerungswachstum“ in natürlichen Systemen zu beschreiben. Aber der Bereich
ihrer Gültigkeit wird eingeschränkt. Es kann also sein, dass eine mathematische
Beschreibung einen Naturvorgang unter bestimmten Randbedingungen sinnvoll
erfasst, und dass wir plötzlich (und nicht vorhersehbar) bei sehr kleinen
Veränderungen, beim nächsten Schritt unversehens im Chaos landen.
Die Lehre für die Naturwissenschaft heißt hier. Unsere
Rechenmodelle von der Welt gelten nicht immer und überall. Manchmal kann die
Naturwissenschaft nur noch (durch Probieren) ausloten, für welche Bereiche der
Wirklichkeit ihre Formeln sinnvolle Beschreibungen liefern – und wo die
Berechnungen im Chaos enden. Exakte, eindeutige Berechnungen und Prognosen
sind nicht (mehr) immer möglich.
5. Versuch einer Zusammenfassung
Nicht überall ist CHAOS ...
1. Auch im neuen Weltbild gilt:
Die Naturgesetze bleiben in Geltung, die Welt verhält sich deterministisch.
2. ABER:
Manchmal ist die Welt, sind Systeme mathematisch nicht eindeutig in ihrem zukünftigen
Verhalten zu berechnen.
Das gilt besonders
+ für komplexe Systeme
+ für instabile Grenzbereiche und Übergangs-Zustände
+ wenn Entwicklungen sich über lange Zeiträume erstrecken.
Die Chaosforschung zeigt an einem neuen Beispiel, dass es
Grenzen der Naturwissenschaft gibt. Sie macht aber Naturwissenschaft und die
Beschäftigung mit ihren Einsichten nicht etwa überflüssig!
Die Naturgesetze gelten weiter. Die Welt hält sich in weiten
Teilen an die von Menschen enträtselten „Spielregeln“ (vielfach zuverlässig
funktionierende Technik mag hier als Beweis dienen). Die Weltsicht der
klassischen Naturwissenschaft ist nicht falsch, aber sie ist
ergänzungsbedürftig:
Wenn wir heute Anlass haben, über CHAOS in unserer Welt zu reden, bedeutet das
nicht absolutes Unwissen, sondern lediglich eingeschränktes Wissen. Die Welt
bleibt deterministisch. In der Rückschau ist jeder Naturvorgang schlüssig zu
erklären. Aber die Prognosen, die Vorhersagen für das zukünftige Verhalten,
sind nicht immer eindeutig. Auch „chaotische“ Systeme sind zwar noch im
Prinzip berechenbar, weil sie strikten und allgemeinen Gesetzen gehorchen
(„deterministisch“). Sie sind aber faktisch nicht berechenbar, da dies
eine beliebig genaue Bestimmung aller einwirkenden
Ausgangsbedingungen voraussetzen würde – das ist aber nicht zu verwirklichen
und führt zu „chaotischen“ Prognosen.
Das gilt besonders für
- komplexe
Systeme (die NW versucht im Idealfall, alle äußeren störenden Einflüsse
auszublenden; wir merken: manchmal funkt uns der „Rest des Universums“
doch dazwischen!)
- instabile
Grenzbereiche und Übergangssituationen (ein System steht gewissermaßen auf
der Kippe, es kann sich in der einen Richtung oder auch in einer ganz
anderen weiter entwickeln, hier kann ein unmerklich kleiner Anstoß den
Ausschlag geben)
- Entwicklungen,
die sich über lange Zeiträume erstrecken.
Die grundsätzlichen Einsichten der Chaosforschung sind
längst auch in Schullehrbüchern gelandet.
„Trotz aller
Berechenbarkeit bleibt immer ein Rest Offenheit, Freiheit ... aber auch
Unsicherheit und Unwissenheit“
(Physiklehrbuch Oberstufe
Westermann S.133)
Man liest erstaunt in einem naturwissenschaftlichen Lehrbuch
„unwissenschaftliche“ Begriffe. Da ist von Unsicherheit, Freiheit, Offenheit
die Rede.
Einsichten der CHAOS-Forschung
-
Anlass zum Nachdenken über unsere Bilder von der Welt
+ Selbstverständnis der modernen Naturwissenschaft
(Erinnerung an die Grenzen
menschlicher Erkenntnisfähigkeit, Mahnung zur Bescheidenheit)
+ Weltverständnis des Menschen im 21. Jahrhundert
(die Welt ist für uns nicht
umfassend zu verstehen,
beim Eingreifen in die Welt können wir
nicht alle Wirkungen mit 100%iger Sicherheit abschätzen,
die Zukunft der Welt ist offen: für
Überraschungen und zur Gestaltung)
+ Bedeutung für mein Gottesverständnis?
(Finde ich Geborgenheit in der
Welt eines „Uhrmacher-Gottes“, deren Lauf festgelegt ist, oder Freiheit und
Unsicherheit zugleich in einer Schöpfung, die eine offene Zukunft hat?)
Die
Einsichten der Chaosforschung haben relativ wenig direkten Bezug zu unserem
Alltag.
Es geht mehr um philosophische Auswirkungen, dabei aber kommen sehr
grundsätzliche Fragen in den Blick.
A) Haben
die Entdeckungen der Chaosforschung Auswirkungen auf das Selbstverständnis der
modernen Naturwissenschaft?
Der Mensch wird an die Grenzen
seiner Erkenntnisfähigkeit erinnert, zur Bescheidenheit gemahnt.
Die Naturwissenschaft ist nicht für die gesamte Wirklichkeit dieser Welt
zuständig. Sie kann nicht alles genau beschreiben, erkennen und erklären.
Naturwissenschaft ist nicht allmächtig. Und sie findet nicht zu endgültigen
Wahrheiten. Ihre Erkenntnisse sind immer vorläufig und verbesserungsbedürftig.
Und genau eine solche Korrektur passiert jetzt. Die Naturwissenschaft selbst
ist auf die CHAOS-Phänomene gestoßen. Und nun muss sie ihre Grenzen, ihre
Zuständigkeit neu definieren.
B) Was bedeuten die Entdeckungen der Chaosforschung für das
Weltverständnis des modernen Menschen?
Nicht alles in der Welt ist für uns Menschen eindeutig erkennbar. Wir
können in die Welt nicht immer zielgenau eingreifen, um sie zu beherrschen.
Manches kriegen wir nicht in den Griff, oder es gibt unerwartete „Risiken und
Nebenwirkungen“. Das mahnt zur Vorsicht bei der technischen Umgestaltung der
Welt. Vielleicht haben uns die Erfahrungen mit dem Ozonloch oder einem
möglichen Klimawandel (Treibhauseffekt) nachdenklich gemacht.
Diese Unsicherheiten haben auch einen positiven Aspekt: Die Zukunft der Welt
ist grundsätzlich (noch) nicht festgelegt, sie ist offen. Das heißt aber: wir
müssen und wir dürfen immer auf Überraschungen gefasst sein. Und die Welt ist
auch offen zur Gestaltung durch uns Menschen. Auch kleine Schritte können den
Lauf der Welt verändern („Schmetterlinge sein“).
C) Haben die Einsichten der Chaosforschung Bedeutung auch
für meinen Glauben?
Was bedeuten die Einsichten der Chaosforschung für mich als Christ?
Welche Fragen werfen sie auf, für meinen Glauben, für mein Gottesbild, für mein
Gottesverständnis?
Hier ist zur Vorsicht zu mahnen. Der Glaube muss nicht jeder modernen Strömung
des Zeitgeistes stürmisch um den Hals fallen. Die Gefahr einer zu schnellen
Anpassung deutet sich z.B. an, wenn das Deutsche Pfarrerblatt von einer
„Chaos-Theologie“ berichtet, einem „nichtlinear handelnden Gott“.
Es sei daran erinnert, dass Einstein (damals angesichts der Erkenntnisse der
Quantenphysik) gesagt hat: GOTT WÜRFELT NICHT! Ist das nun anders, würfelt Gott
doch?
Was habe ich für ein Bild von Gott?
Erlebe ich Gott als den großen Uhrmacher, als Schöpfer eines Uhrwerks, einer
Welt, in der alles vorherbestimmt ist? Empfinde ich in einer so verstandenen
Schöpfung tiefe Geborgenheit, weil alles von Gott gewollt und gewirkt ist („Er
hält die ganze Welt in seiner Hand“). Bin ich dankbar, von meinem ersten
Atemzug bis zu meinem Tod von Gott geführt und getragen zu werden, ihn für
jeden Schritt in meinem Leben verantwortlich zu wissen? Aber ist Gott dann
nicht letztlich auch für mein Fehlverhalten verantwortlich? Erweist sich in
einem solchen Gottesverständnis meine Willens-Freiheit, die Fähigkeit,
Entscheidungen für mein Leben zu treffen, letztlich doch als Illusion? Bin ich
eine Marionette?
Oder ist das meine Vorstellung, meine Erfahrung mit Gott:
dass er seiner Welt und seinen Geschöpfen wirkliche Freiheit gibt, dass die
Welt, die Schöpfung, mein Leben eine offene Zukunft haben? Das aber wäre ein
Gott, der ein Stück weit auf seine Allmacht verzichtet. Geht seine
Zurückhaltung so weit, dass er den Menschen zugesteht, eigene Wege zu suchen
und zu gehen, auch wenn sie der Weg von Gott wegführt, wenn sie ihr Leben
verfehlen? Ich denke hier an das biblische Gleichnis vom verlorenen Sohn (Lukas
15,11ff.): Der Vater (Gott) schenkt seinem Sohn volle Freiheit, lässt in die
Welt gehen, auf seinem eigenen Weg. Und der Sohn scheitert. Dass er danach zu
seinem Vater zurückkehrt - das ist ein möglicher Ausgang der Geschichte;
das Scheitern hätte auch endgültig sein können. Der Vater ist nur glaubwürdig,
wenn er es mit der geschenkten Freiheit wirklich ernst gemeint hat, den
weiteren Gang der Geschichte nicht kennt, nicht eingreift, jeden Ausgang zu
akzeptieren bereit ist. Begegnet uns hier ein Gott, der seinen Geschöpfen
wirkliche Freiheit gibt, der sich überraschen lässt?
In einem solchen Gottesverständnis ergäbe sich auch eine
Aufgabe für uns. Wir dürfen die uns von Gott geschenkten Begabungen nutzen, wir
dürfen die Welt entdecken und gestalten, wir können Entscheidungen treffen,
wohin wir unsere Schritte richten wollen, aber dann haben wir auch
Verantwortung zu tragen für die Konsequenzen unseres Tuns und sollten nicht zu
schnell nach dem allmächtigen Gott rufen.
Wie geht es mir mit den Anfragen aus der Chaosforschung –
als Mensch im 21. Jahrhundert, als Naturwissenschaftler, oder im Nachdenken
über mein Gottesbild ?
6. Warnung
vor Chaos-Kult und Scharlatanen
Liefert die Chaosforschung nun endlich die eine, alles umfassende
Welt-Erklärung?
Ein gläubiges Publikum
nötigt manche Forscher, in ihre Erkenntnisse viel mehr hineinzudeuten, als sie
wirklich wissen (können).
Da wird in der Deutung von Chaosphänomenen oft grob vereinfacht
oder fahrlässig verallgemeinert.
Scharlatane treten auf, die zwar nichts von Chaosforschung, aber viel von ihrer
Vermarktung verstehen.
Darf man die Muster, die sich aus dem Verhalten von Atomen, Hefezellen, mathematischen
Gleichungen ableiten, ungeniert übertragen auf die menschliche Gesellschaft und
ihre Kultur, auf die Dynamik von Konzernen, Märkten und Moden?
Und wenn das geschieht, begegnen wir hier nicht neuen Alleinvertretungsansprüchen?
Da legt sich schnell der Verdacht nahe, dass wir es mit Ideologie zu tun haben
könnten (Ideologie liegt immer dann vor, wenn jemand den Anspruch erhebt,
allein im Besitz von nicht mehr hinterfragbaren Antworten und endgültigen
Wahrheiten zu sein).
Einige merkwürdige Beispiele seien genannt:
·
Ein Firmenboss
streut in der Mitarbeiterversammlung chaosstiftende Mitteilungen (die
Konkurrenz hat den Durchbruch geschafft; die Märkte kommen ins Trudeln ...),
um durch die Verwirrung vielleicht schöpferische Kreativität freizusetzen.
·
Ein japanischer
Druck aus dem 18. Jahrhundert wird – wegen seiner Ähnlichkeit mit modernen
Computergrafiken aus der Chaosforschung - als visionäre Vorausahnung und
Ausdruck der großen Einheit der Welt gedeutet (siehe Abbildung).
·
Ein Musiker lässt
sich zu einer „fraktalen Seepferdchen-Etude für Klavier“ inspirieren.
·
Zeitgenössische
Gedichte werden auf „Chaos-Rhythmen“ untersucht.
·
Auch Ideologen
der „reinen“ Marktwirtschaft berufen sich auf Chaos-Forschung („nur ja keine
ökologisch oder sozial steuernden Eingriffe – da ist nur Chaos zu erwarten –
lasst das freie Spiel der Marktkräfte zu, sie finden ihren Weg“)
Und da ist noch der schöne Schein der Bilder vom Chaos.
Sie werden oft in einem Atemzug mit der Chaosforschung genannt.
Bei diesen Bildern geht es um fraktale Geometrie, um Selbst-Ähnlichkeit.
Verwandte Muster werden entdeckt, die überall in der Mikro- und Makrowelt
ähnlich zu finden sind. Die Verteilung der Sahne im Kaffee erinnert an das Bild
einer Galaxie. Verzweigungen von Blitzen, Ästen, Wurzeln, Nervensystemen sehen
aus wie manche Grafiken, die ein Computer generiert hat. Die Muster von Blüten
erinnern an Chaos-Fraktale.
Wird hier eine neugefundene Harmonie im Kosmos immer wieder
bestätigt?
Fraktale und Chaos werden oft in einem Atemzug genannt, obgleich
sie völlig Unterschiedliches bezeichnen und nicht ohne geistige Anstrengung in
Verbindung zu bringen sind: CHAOTISCH ist ein PROZESS hinsichtlich seiner
DYNAMIK. FRAKTAL ist ein OBJEKT hinsichtlich seiner GEOMETRIE.
Durch die Bilder aus dem Computer wird eine verlockende Brücke
wird hergestellt zwischen rationaler wissenschaftlicher Einsicht und
emotionalem Empfinden. Chaos und Ordnung erscheinen ästhetisch schön und
harmonisch miteinander verknüpft. Und mitten im Chaos erscheint zuverlässig
und faszinierend das so genannte "Apfelmännchen".
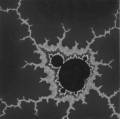Das „Apfelmännchen“
Ebene
der komplexen Zahlen (Wurzel aus -1 = i mit dabei),
Gleichungen nach Muster zn+1 = zn2 + c,
Lösungen werden eingefärbt:
a) endliche Lösungen = schwarz
b) unendliche Lösungen: farbig unterschiedliche Tönung je nach Zeit-Dauer bis
zur „Entscheidung" des Computers
c) im Grenzbereich: Chaos
Das Sehen ist einer der wichtigsten Sinne des Menschen (Menschen
sind so auch „steuerbar“, z.B. durch emotionale Färbungen). Wir Menschen
versuchen immer, bei gezeigten Bildern uns bekannte Dinge aus Natur oder
Technik zu assoziieren. Einer der Gründungsväter der Chaos-Forschung in den
1980er Jahren, der Bremer Mathematiker Peitgen, erzählte, dass, als er in den
60er Jahren Mathematik studierte, Visualisierungen (bildliche Darstellungen)
mathematischer Sachverhalte streng verpönt waren, da sie immer auch Anlass zu
(Miss-)Interpretationen geben können. Ein „Bilderverbot“ für Mathematiker?
Kritische Spötter meinen, dass der wissenschaftliche
Erklärungswert der Computer-Grafiken etwa so groß ist, als wenn wir
Tapetenmuster vor uns hätten ...
Die zuletzt gemachten Einschränkungen waren zur Abrundung des Themas
nötig.
Damit soll aber nicht alles in Frage gestellt werden, was ernsthafte
Chaosforschung bisher entdeckt hat.
Was bleibt, ist Nachdenklichkeit: die Welt ist doch wohl anders, als wir noch
vor wenigen Jahren glaubten!
„ZUFALL ist
das unberechenbare Geschehen, das sich unserer Vernunft und Absicht
entzieht.“
(Gebrüder
Grimm, Deutsches Wörterbuch)
6. Anhang
6.1. Klassischer
Determinismus und Grenzen der Ordnungssuche
(aus: Gerhard Vollmer, UNIVERSITAS 8/1991 S.768f.)
Klassischer
Determinismus
Das klassische Ideal einer erfolgreichen Ordnungssuche
stellt der Laplacesche Dämon dar:
„Ein Geist, der (für einen
Augenblick alle Kräfte kennte, welche die Natur beleben, und die gegenseitige
Lage aller Wesenheiten, aus denen die Welt besteht, müßte, wenn er zudem
umfassend genug wäre, um alle diese Angaben der (mathematischen) Analyse zu
unterwerfen, in derselben Formel die Bewegungen der größten Himmelskörper und
die der leichtesten Atome überblicken. Nichts wäre ungewiß für ihn, und Zukunft
wie Vergangenheit wären seinen Augen gegenwärtig.“
Laplace behauptet also, daß unter gewissen Bedingungen die
ganze Welt berechenbar wäre. Es ist lehrreich, sich die Voraussetzungen und die
Konsequenzen dieses epistemischen Ideals klarzumachen. Dies versuchen wir in
der Tabelle.
In dieser Darstellung wird vom Prinzip der schwachen
Kausalität Gebrauch gemacht: Gleiche Ursachen haben gleiche Wirkungen.
Die klassische Physik hat stillschweigend ein weit stärkeres Prinzip
zugrundegelegt, das Prinzip der „starken" Kausalität: Ähnliche
Ursachen haben ähnliche Wirkungen. Danach wirken sich kleine Abweichungen
in den Anfangsbedingungen auch auf die späteren Zustände des betrachteten
Systems nur geringfügig aus; kleine Ursachen haben nicht beliebig oder
unvorhersagbar große Wirkungen. Laplace hat dieses Prinzip nicht formuliert;
wir dürfen aber annehmen, daß er es, wie die spätere Physik auch,
uneingeschränkt bejaht hätte. Bei den Prämissen in der Tabelle entfällt dann
die Forderung der absoluten Genauigkeit, und deshalb dürfen dann auch die
Rechenergebnisse entsprechende, d. h. mit den anfänglichen Abweichungen
vergleichbare Ungenauigkeiten aufweisen.
Tabelle:
Voraussetzungen und Konsequenzen des klassischen Determinismus
WENN die Welt
+ deterministisch wäre und
+ ausschließlich aus
(untereinander wechselwirkenden) Teilchen bestünde,
wenn die Newtonsche
Bewegungsgleichung m • b = K uneingeschränkt gültig wäre,
wenn wir
+ alle Naturgesetze, insbesondere
alle Kraftgesetze, und
+ alle Rand- und
Anfangsbedingungen zu einem bestimmten Zeitpunkt (d. h. bei Gültigkeit der
Newtonschen
Gleichung die Orte und
Geschwindigkeiten aller Teilchen)
+ mit absoluter Genauigkeit
kennten und
wenn wir
+ alle diese Daten
speichern,
+ mathematisch verarbeiten
und
+ schnell genug
+ alle einschlägigen
Gleichungen lösen könnten,
DANN wäre
nicht nur der Lauf der Welt
+ in allen Einzelheiten
+ eindeutig bestimmt
(gleiche Ursachen haben gleiche Wirkungen),
sondern dann könnten wir
(oder wenigstens der Laplacesche Dämon oder ein gigantischer Supercomputer)
sogar
+ alle Ereignisse
+ der Vergangenheit und der
Zukunft rechnerisch ermitteln.
Grenzen
der Ordnungssuche
Die Suche nach Ordnung und Struktur, nach Regelmäßigkeiten
und Naturgesetzen, war, das lehrt die Wissenschaftsgeschichte, recht
erfolgreich. Aber eine Garantie, daß sie immer und überall zum Ziel führen
werde oder gar müsse, gibt es nicht. Tatsächlich haben sich längst auch Grenzen
dieses Ansatzes gezeigt. Sie liegen zum einen in der Verfaßtheit der realen
Welt, zum anderen in den Möglichkeiten (oder vielmehr in den Beschränkungen)
des erkennenden Subjekts. Sieht man genau hin, so erweisen sich alle Prämissen
des Laplaceschen Determinismus, soweit sie nicht sowieso nur epistemische Idealisierungen
unbeschränkten Wissens und Könnens darstellen, als verfehlt. Dies kann hier
allerdings nur noch durch eine Aufzählung belegt werden.
·
Die Welt ist nicht deterministisch. Nach der üblichen
Deutung der Quantenphysik gibt es absoluten Zufall (und damit z.B. für den Zeitpunkt eines spontanen Kernzerfalls nicht
nur keine Ursache, sondern auch und erst recht keine Erklärung).
·
Die Welt besteht nicht nur aus Teilchen; sie enthält
auch Felder. Der klassische Determinismus läßt sich allerdings auf (klassische) Felder übertragen, so daß die Entdeckung von
Feldern im 19. Jahrhundert den Determinismus noch nicht ernsthaft gefährdete.
·
Die Newtonsche Bewegungsgleichung ist nicht
universell anwendbar, insbesondere nicht auf Teilchen ohne Ruhemasse, etwa auf Photonen.
·
(Ob wir alle Kraftgesetze kennen
oder kennen könnten, darf offenbleiben; daß es so sei, hat ja auch Laplace
nicht behauptet.)
·
Messungen können den Zustand eines Systems verändern (stören,
in einer Weise, die weder vorhergesagt noch nachträglich bestimmt
werden kann.
·
Ort und Impuls eines einzelnen Teilchens sind nicht
nur nicht gleichzeitig beliebig genau meßbar; reale Systeme haben überhaupt nicht scharfen Ort und Impuls. Die Quantenphysik
definiert den Zustand eines Teilchens deshalb anders als die klassische
Physik.
·
Absolute Genauigkeit einer Messung würde bei einer kontinuierlichen
Größe (wie Ort, Zeit, Geschwindigkeit) die empirische
Bestimmung einer reellen Zahl, also von unendlich vielen Dezimalstellen
bedeuten. Das ist nicht realisierbar.
·
Daß die Prämissen der umfassenden Datenspeicherung,
Datenverarbeitung und Rechengeschwindigkeit für uns Menschen nicht erfüllbar
sind, wußte natürlich auch Laplace; gerade deshalb hat er ja einen Geist mit übermenschlichen Fähigkeiten eingeführt. Jedoch
durfte Laplace noch davon ausgehen, daß alle mathematischen Probleme durch
angebbare Verfahren, also letztlich algorithmisch, gelöst werden können.
Heute wissen wir, daß auch diese Annähme falsch ist. Für manche Probleme konnte
gezeigt werden, daß es für sie keinen Lösungsalgorithmus geben kann. Außerdem
ist für viele durchaus realistische Probleme ein Lösungsweg zwar bekannt;
jedoch würde er selbst den ins Auge gefaßten kosmischen Supercomputer
nachweislich weit überfordern. Und einen
eleganteren Lösungsweg gibt es dabei nicht; in einigen Fällen ist das bewiesen,
in anderen ist es höchstwahrscheinlich.
·
Das Prinzip der starken Kausalität ist nicht erfüllt.
Wie die Untersuchungen an chaotischen Systemen zeigen, können auch beliebig kleine Änderungen der
Anfangsbedingungen immer noch zu unübersehbaren Abweichungen in späteren
Zuständen führen. Bei solchen Systemen ist trotz ihrer deterministischen
Struktur (also trotz schwacher Kausalität) keine zuverlässige
langfristige Prognose möglich.
Es sind also drei Entwicklungen in
der modernen Wissenschaft, die den Laplaceschen Dämon, den klassischen Determinismus
und damit die traditionelle Ordnungssuche ganz entscheidend in Frage stellen:
Quantenphysik, Algorithmentheorie (Metamathematik) und Chaos-Theorie.
6.2.
Auswirkungen der Chaosforschung auf theologische Überlegungen?
(aus: Achtner, Wolfgang: Die Chaostheorie, EZW-Texte Nr. 135 (1997), S.42ff.)
A) Theologie des angelsächsischen Sprachraums
„Das theistische Gottesbild (in der Theologie
des angelsächsischen Sprachraums weit verbreitet), vereinbar mit der
biblischen Tradition des Handelns Gottes in der Geschichte, rechnet einerseits
mit Eingriffen Gottes in die Natur, andererseits herrscht nach dem Siegeszug
der Naturwissenschaft die Vorstellung, dass Naturgesetze den Ablauf des
Geschehens in der Natur festlegen. Daraus ergibt sich das Problem, wie die
Freiheit göttlichen Eingreifens mit dem Determinismus der Naturgesetze in
Einklang gebracht werden kann. Im Prinzip gibt es zwei Lösungsmöglichkeiten ...
Entweder Gott setzt die Naturgesetze für die Dauer seines Eingreifens außer
Kraft, oder die Erklärung der Natur weist Lücken auf. Beide Optionen sind
intellektuell unbefriedigend und wirken auch ein bisschen kleinlich, wenn sie
Gott nur noch den Bereich überlassen, den der Mensch noch nicht meistert
(„Lückenbüßergott“). Aus dem geschilderten Dilemma scheint nun die moderne
Physik einschließlich der Chaostheorie einen Ausweg zu bieten. Bereits die Unschärferelation
der Quantenmechanik besagt, dass es prinzipiell unmöglich ist, je zwei
miteinander gekoppelte Größen, deren Produkt die Einheit einer Wirkung hat
(Ort x Impuls; Drehimpuls x Winkel; Energie x Zeit), gleichzeitig beliebig
genau zu bestimmen. Wenn aber schon eine Größe nicht genau quantifiziert
werden kann, dann kann auch ihre Wirkung nicht prognostiziert werden. Mithin
scheint hier eine Lücke in der durchgehenden Determiniertheit der Natur vorzuliegen.
Dieser Sachverhalt ermöglicht nun aber die Möglichkeit, eine Einwirkung Gottes
in die Natur zu denken, ohne dass damit die Naturgesetz selbst außer Kraft
gesetzt werden müssten. Auf eine solche, in der Schöpfung gewissermaßen vorgesehene
Lücke für die Interaktion Gottes mit der Welt, ist der Fragehorizont für die
Rezeption der Chaostheorie im angelsächsischen Sprachraum ausgerichtet ...“
„... ziehen den Schluss, die theologische Bedeutung der Chaostheorie in
der Wirksamkeit Gottes im Prozess in Übereinstimmung mit den
Naturgesetzen in Anspruch zu nehmen ...“
„... Tendenz festzustellen, das starre theistische Gottesbild zugunsten
einer stärkeren Betonung der Immanenz Gottes aufzubrechen.“
„... interpretiert die Chaostheorie als holistische Theorie (whole-part),
in der das Ganze den Teil beeinflusst (top-down-causality = von oben nach
unten wirksame Kausalität). Gott ist dann derjenige, der den einzelnen
Geschöpfen in Anlehnung an den physikalischen Begriff der Randbedingung
existenzerschwerende Zwänge auferlegt, um sie zur Evolution (=Entwicklung,
Veränderung) zu nötigen, ohne den Verlauf im einzelnen festzulegen. So bleibt
Gottes Freiheit (und) die relative Autonomie der Geschöpfe gewahrt, ohne auf
einen Einfluss Gottes verzichten zu müssen. Der holistische Charakter der
Chaostheorie dient ... dabei als Metapher, Transzendenz und Immanenz Gottes
zusammenzudenken. ... nicht danach suchen, Gottes Tat in der Welt zu
verstehen, sondern versuchen, sich die Welt als Gottes Tat vorzustellen ...“
B) Rezeption im deutschen Sprachraum
(wenig Anknüpfungspunkte wegen kritischer Tradition gegenüber
theistischer und natürlicher Theologie; Ansatzpunkte am Beispiel von A.
Ganosczy:)
„... Das Chaotische ist keine eigenständige Gegenmacht, die von Gott erst
wie in den außerbiblischen Mythen niedergekämpft werden muss. Vielmehr lässt
Gott das Chaotische zu, verzichtet gewissermaßen auf seine instantane (= sich
sofort auswirkende) linear kausale (= auf klare Ziele ausgerichtete) Allmacht
des Schaffens und gestattet dem Geschaffenen einen Freiraum zur Selbstwerdung.
Dieser Selbstwerdungsprozess läuft keineswegs linear kausal ab, sondern
durchläuft chaosähnliche Zwischenphasen, die eine durchaus auch
konfliktträchtige cooperatio (= Zusammenarbeit, Zusammenspiel) – gut
katholisch - des Geschöpfs mit dem Schöpfer zulässt. Der Endpunkt des dieses dynamischen
Selbstwerdungsprozesses ist dabei offen, weil Gott die Freiheit der
Selbstwerdung bis hin zur Konsequenz des Scheiterns seiner Schöpfung belässt.
Was früher einmal die von Gott gesteuerte Heilsgeschichte war, und sei sie in
ihren Verschlingungen, Ab- und Umbrüchen,, Rückschlägen und Neueinsätzen als
eine Heilsgeschichte noch so schwer erkennbar, wird nun zum offenen
Prozess der Selbstwerdung der Schöpfung. Damit lautet Ganoczys entscheidendes
theologisches Argument: Verzicht auf die Allmacht Gottes. ...“
(Kritik:) „... Es scheint, dass Ganoszy durch seine ... metaphorische
Sprechweise den eigentlichen Witz der Chaostheorie, die Scheinparadoxie des
deterministischen Chaos, nicht wirklich wahrnimmt. Wir sahen, dass man in der
Chaostheorie streng unterscheiden muss zwischen Determinismus und Voraussagbarkeit.
Alle Prozesse der Chaostheorie sind streng deterministisch, also klassisch,
aber nur aufgrund der sich aufschaukelnden Rückkopplungsprozesse nicht
voraussagbar. ... Wir haben mehrfach betont, dass die Chaostheorie eine
klassische deterministische Theorie ist. D.h. die Vergangenheit determiniert
die Zukunft im strengen Sinne, auch wenn die Zukunft nicht vorausgesagt werden
kann und daher den Anschein erweckt, offen zu sein. Wir können diesen
Sachverhalt auch so formulieren, dass wir sagen: Die Prozesse, die die
Chaostheorie beschreibt, sind vergangenheitsorientiert. Diese Grundstruktur ist
aber im biblischen Glaubensvollzug ... keineswegs gegeben. Im Gegenteil kann
man sagen, dass der Glaubensvollzug zukunftsorientiert ist. Um es noch
schärfer zu sagen: Die Zukunft, die Verheißungen Gottes, bestimmen die
Gegenwart, nicht die sich in Rückkopplungen akkumuliernde Vergangenheit. ... Die Gottesherrschaft ist keine
innerweltlich evolvierende (= sich entwickelnde) Größe, aber sie ist als eine
nahe und dennoch zukünftige nichtsdestoweniger eine Wirkgröße, die die
Gegenwart qualifizierend bestimmen kann für denjenigen, der sich glaubend
darauf einlässt. Daher verknüpft Jesus in seiner Verkündigung die Ansage der
Nähe der Gottesherrschaft mit dem Ruf zur Umkehr: >Die Zeit ist erfüllt und
das Reich Gottes ist nahe herbeigekommen. Kehrt um und glaubt an das
Evangelium (Mk 1,15)< Eine solche Zeitstruktur hat nun in der Tat nicht nur
nicht den Charakter der Voraussagbarkeit, sondern auch nicht den Charakter des
Determinismus. Und damit ist eine solche Zeitstruktur prinzipiell nicht im
begrifflichen Rahmen der Chaostheorie aussagbar. ... Wenn die Chaostheorie im
oben genannten Sinne vergangenheitsorientiert ist, also mit der
Zukunftsstruktur des Glaubens nicht kompatibel ist und umgekehrt auch für einen
externen transzendenten Impulsgeber (= einen Schöpfer-Gott, der „außerhalb“
und „jenseits“ der natürlichen Welt steht) keinen Raum hat, fragt sich in der
Tat, ob die Chaostheorie überhaupt einen theologischen Ort haben kann. ...“
(Neues aus der Chaosforschung für die Theologie?:) „... Interessant ist
sicher der Gedanke, den zulassenden, gewährenden Gott mit dem Gedanken der Selbstorganisation,
d.h. der relativen Autonomie des geschöpflichen Seins in Verbindung zu bringen
– etsi deus non daretur (= als ob es Gott nicht gäbe)! Schwierig wird es nur
dann wieder, Gottes Interventionen (= Eingreifen) auszusagen, wenn man ihn
nicht ganz im Werdeprozess aufgehen lassen will.“
(Rechtfertigungslehre:) „... da eine Erlösung im vollen Sinne in der
Immanenz ... nicht möglich ist, bleibt der Mensch auf die fremde (= von außen
kommende, nicht verdiente) Gerechtigkeit Gottes angewiesen. Aus dieser
Perspektive erscheint auch die Rechtfertigungslehre als kritischer Faktor
gegenüber einer zu vorschnellen Rezeption der Chaostheorie in die christliche
Anthropologie. ... Vom Standpunkt der Rechtfertigungslehre geht ... der Mensch
religiös gesehen nicht in seinem Handeln auf, auch wenn sich seine
Subjektivität und Individualität erst durch Handlungsvollzüge konstituiert.
...“
„Die Zukunft ist vor allem im Bereich menschlichen Planens, Gestaltens
und Hoffens offen. Damit liegt in diesem menschlichen Bereich eine Zeitstruktur
vor, die prinzipiell von der vergangenheitsorientierten Zeitstruktur der Chaostheorie
verschieden ist. ... im Vollzug menschlicher Zeitgestaltung determiniert die
Zukunft die Gegenwart. Im religiösen Bereich manifestiert sich das in der
Gestalt des Glaubens und der Hoffnung, im psychologischen Bereich in Gestalt
menschlicher Intentionalität, im ökonomisch-gesellschaftlichen Bereich als
Planung. Daher sollte man bei allen Anwendungen der Chaostheorie. die
menschliches Planen und Handeln abzubilden vorgeben, äußerste Vorsicht walten
lassen. ...“
7. Literatur:
Achtner, Wolfgang: Die Chaostheorie, EZW-Texte Nr. 135 (1997), Ev. Zentralstelle
für Weltanschauungsfragen, Auguststr. 80, 10117 Berlin
Bublath, Joachim: Chaos im Universum, Droemer München 2001
Breuer, Reinhard (Hrsg.): Der Flügelschlag des Schmetterlings, Deutsche
Verlagsanstalt Stuttgart 1993
GEO Wissen, Chaos + Kreativität, Gruner und Jahr Hamburg 1990